
Results of models with an elongated domain show that this modification can substantially improve the performance of the PML boundary condition. Then we show that the new PML can be modi-fied easily to include the complex frequency-shifted stretching function. Modeling re-sults show that the performance of our implementation using a standard stretching function is identical to that of the convention-al split-field PML. We present an alternative implemen-tation of a PML that is based on recursive integration and does not require splitting of the velocity and stress fields.
However, in elastic-wave modeling using the conventional PML formulation - based on splitting the velocityand stressfields - it is difficult to adopt a complex frequency-shifted stretching function.
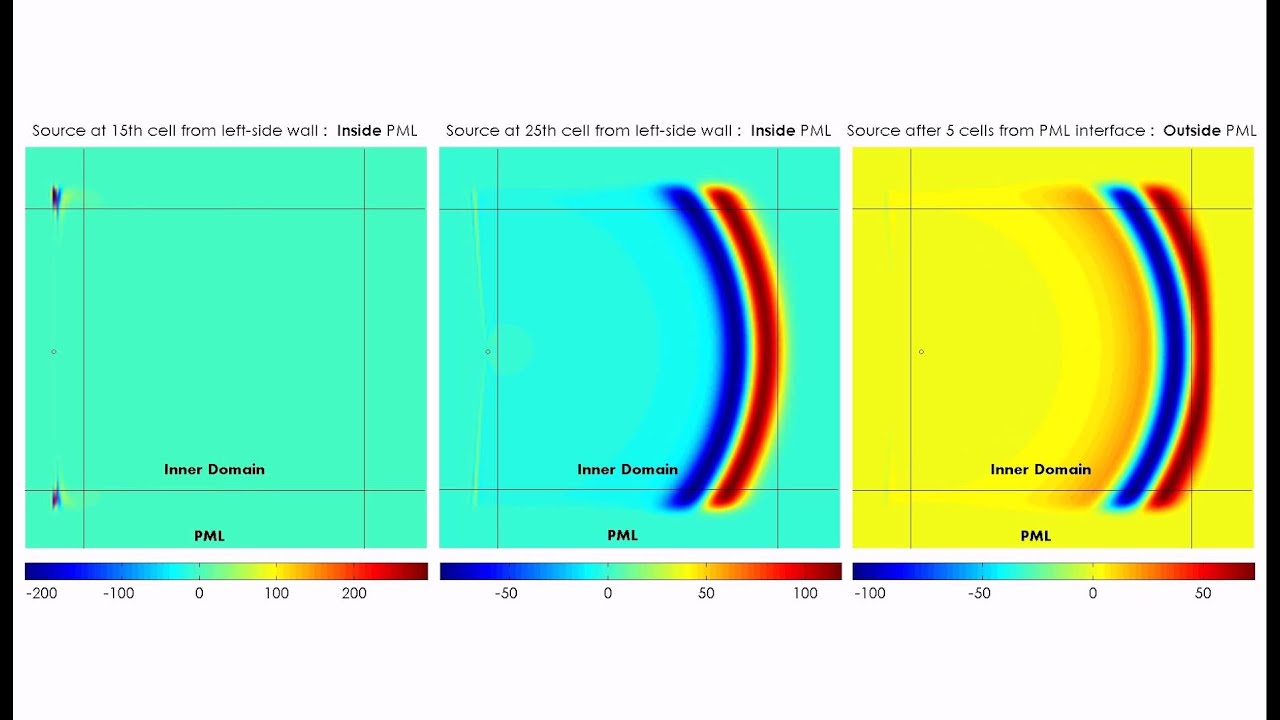
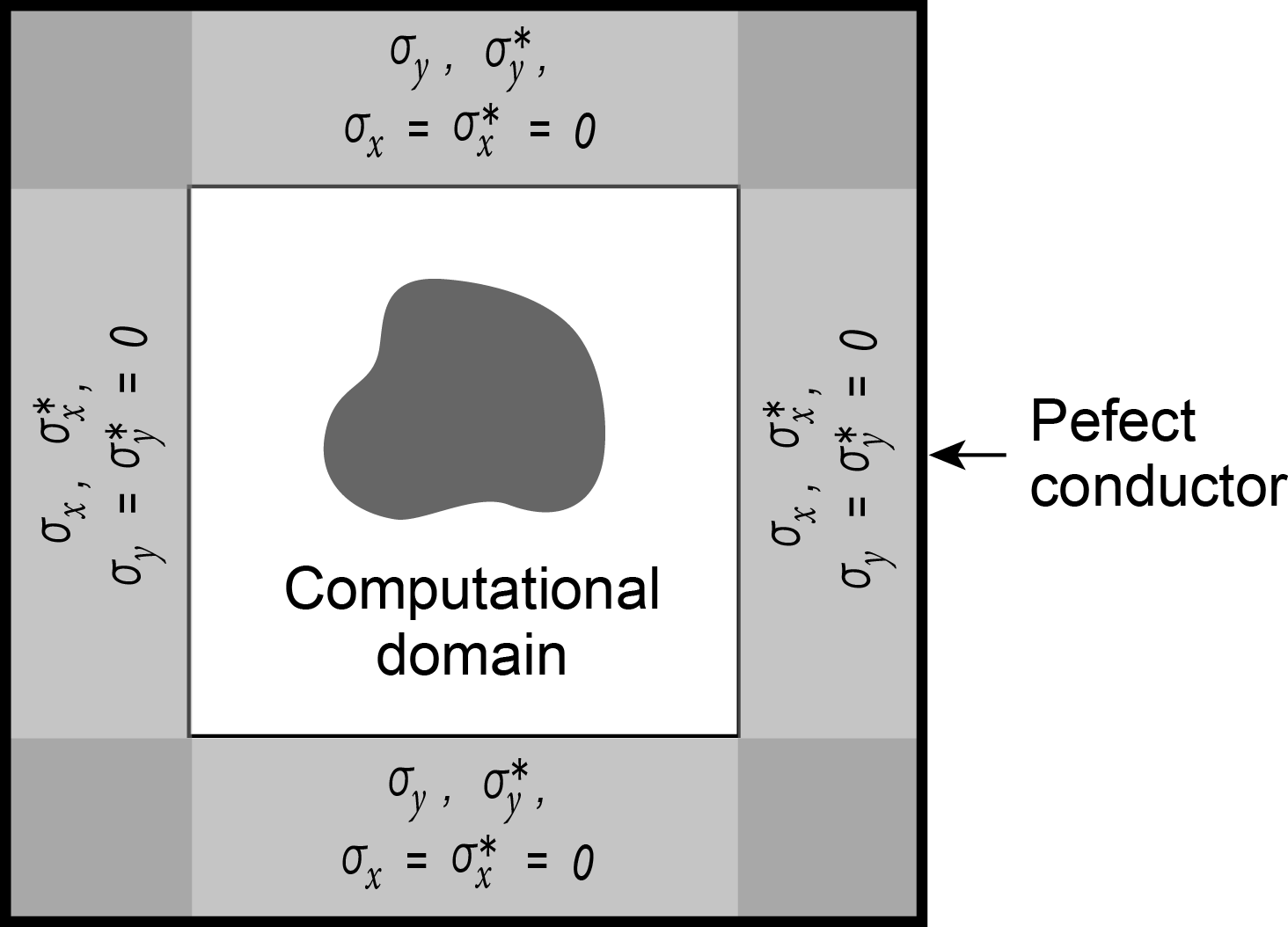
In electromagnetic modeling, similar problems are circumvented by using a complex frequency-shifted stretching function in the PML formulas. In addition, very low frequency waves as well as evanescent waves could cause spurious reflections at the PML interface. An important but rarely addressed limitation of current PML implementations is that their performance is severely reduced when waves are incident on the PML interface at near-grazing angles. The perfectly matched layer (PML) is generally considered to be the best available absorbing boundary condition.

This new higher-order CPML exhibits excellent performance that is comparable to the performance shown by other higher-order PML formu-lations whilst it retains the advantage of a relatively simpler implementation.In finite-difference time-domain (FDTD) modeling of elastic waves, absorbing boundary conditions are used to mitigate undesired reflections that can arise at the model’s truncation boundaries. Obtaining in closed form the corresponding time domain impulse response of the inverse of a number of higher-order PML stretching functions enables the efficient and simple implementation of such higher-order PMLs using recursive convolution, in the same way as it was introduced initially for the complex frequency shifted (CFS) PML. This new higher-order CPML exhibits excellent performance that is comparable to the performance shown by other higher-order PML formu-lations whilst it retains the advantage of a relatively simpler implementation.ĪB - A new simple formulation for incorporating a higher-order perfectly matched layer (PML) stretching function within a convolution PML (CPML) implementation in finite-difference time-domain (FDTD) electromagnetic modelling codes is developed. N2 - A new simple formulation for incorporating a higher-order perfectly matched layer (PML) stretching function within a convolution PML (CPML) implementation in finite-difference time-domain (FDTD) electromagnetic modelling codes is developed. T1 - Higher-Order Convolution PML (CPML) for FDTD Electromagnetic Modelling


 0 kommentar(er)
0 kommentar(er)
